industries news

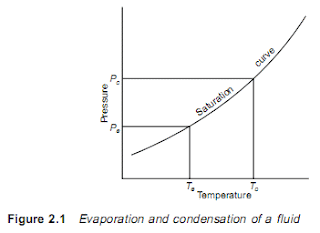
2.1 Basic vapour compression cycle A liquid boils and condenses – the change between the liquid and gaseous states – at a temperature which depends on its pressure, within the limits of its freezing point and critical temperature. In boiling it must obtain the latent heat of evaporation and in condensing the latent heat must be given up again. The basic refrigeration cycle (Figure 2.1) makes use of the boiling and condensing of a working fluid at different temperatures and, therefore, at different pressures. Heat is put into the fluid at the lower temperature and pressure and provides the latent heat to make it boil and change to a vapour. This vapour is then mechanically compressed to a higher pressure and a corresponding saturation temperature at which its latent heat can be rejected so that it changes back to a liquid. The total cooling effect will be the heat transferred to the working fluid in the boiling or evaporating vessel, i.e. the change in enthalpies b

 Refrigeration: The process of removing heat. Air-conditioning: A form of air treatment whereby temperature, humidity, ventilation, and air cleanliness are all controlled within limits determined by the requirements of the air conditioned enclosure. 1.1 Basic physics – temperature The general temperature scale now in use is the Celsius scale, based nominally on the melting point of ice at 0°C and the boiling point of water at atmospheric pressure at 100°C. (By strict definition, the triple point of ice is 0.01°C at a pressure of 6.1 mbar.) On the Celsius scale, absolute zero is – 273.15°C. In the study of refrigeration, the Kelvin or absolute temperature scale is also used. This starts at absolute zero and has the same degree intervals as the Celsius scale, so that ice melts at + 273.16 K and water at atmospheric pressure boils at + 373.15 K. 1.2 Heat Refrigeration is the process of removing heat, and the practical application is to produce or maintain tempera

Eiffel Tower The Eiffel Tower was the world's tallest building when completed in 1889. It was built for the Universal Exposition to demonstrate that iron can be as strong as stone while being infinitely lighter. And, indeed, wrought iron tower is twice as high as the Washington Monument and masonry, however, that weighs 70,000 tons less! It is repainted every seven years, with 50 tons of dark brown paint. The Housing Construction Insurance Called "the father of the skyscraper," the Home Insurance Building was built in Chicago in1885 (and demolished in 1931), was 138 feet high and 10 stories. It was the first building to be used effectively to support a skeleton of steel beams and columns, allowing you to have many windows of traditional masonry structures. But this method of new construction made people worry that the building would fall, leading to the city to halt construction until it could investigate the safety of the structure. The Chrysler Bui

Throughout the history of architecture, has been a constant search for the height. Thousands of workers working in the pyramids of ancient Egypt, the cathedrals of Europe and a host of other towers, all trying to create something impressive. People build skyscrapers primarily because they are convenient - you can create a lot of real estate a relatively small land area. But ego and grandeur often play an important role in the field of construction, as it did in earlier civilizations. Until relatively recently, we could only go as high. After a certain point, it simply was not possible to continue building up. In the late 1800s, new technology is redefining the boundaries. Suddenly, it was possible to live and work in colossal towers, hundreds of feet above the ground. The Twin Towers When the twin towers of World Trade Center were hit on September 11, 2001, seemed at first that could remain standing. But in less than two hours, both towers had collapsed on the floo

Carbon fiber reinforced plastic (CFRP or CRP) is a very strong, light and expensive composite material or fiber reinforced plastic. Similar to glass reinforced plastic, which is sometimes simply called fiberglass, the composite material is commonly known by the name of its reinforcing fibers (carbon fiber). Plastic is most often epoxy, but other plastics such as polyester, vinyl ester or nylon, are also sometimes used. Some compounds contain carbon fiber and glass fiber reinforcement. Less commonly, graphite-reinforced plastic term is also used. Many applications in aerospace and automotive fields, as well as in sailboats, and particularly in modern bikes, where these qualities are important. It is increasingly common in small consumer products, as well as laptops, tripods, fishing rods, frames of racquet sports, stringed instrument bodies, classical guitar strings, and drum shells. Compound The choice of matrix can have a profound effect on the properties of the fi

  Customer intelligence on your iPhone In a recent conversation about predictive analytics, I learned how Wal-Mart Stores used statistical models to better understand the patterns and trends of its customers - and how companies can use this data to a competitive price to dominate a market. Imagine that the same type of customer intelligence, delivered almost instantaneously, in the hands of store managers on-site or corporate executives on your iPhone or IPAD. That's what Medallia, a provider of customer feedback and software performance data, is intended to provide a new offer this week on the heels of the new iPhone announcement in April. Medallia obtains its information from all the requests it receives from the survey hotels, shops, banks and other consumer services. According Medallia CEO and co-founder Borge Hald, these data, when properly extracted, you can let an executive of Nike brand, for example, knowing what customers think about Kobe Bryant new

A compound known as dark pyrophosphite could have been a source of energy that allowed the first life on Earth to form, scientists say now. From the smallest bacteria in the human body complex, all living things require a molecule called ATP-transport energy to survive. Often compared to a "rechargeable battery," ATP chemical energy stored in a form that can be used by organic matter. "You need enzymes to produce ATP, and ATP you need to make enzymes," said researcher Terence Kee, University of Leeds in England. "The question is: Where does the power before any of these things existed? We think the answer may lie in simple molecules such as pyrophosphate, which is chemically very similar to the ATP, but has the potential to transfer energy without enzymes. " Dark, but important Before the theories of how life arose from chemistry only have seen a similar compound, but independent pyrophosphate was known as the predecessor to the more